HyD2002 - Objectifs - Interface graphique - Les objets du modèle - Fichiers d'entrée-sorties - Tutoriel
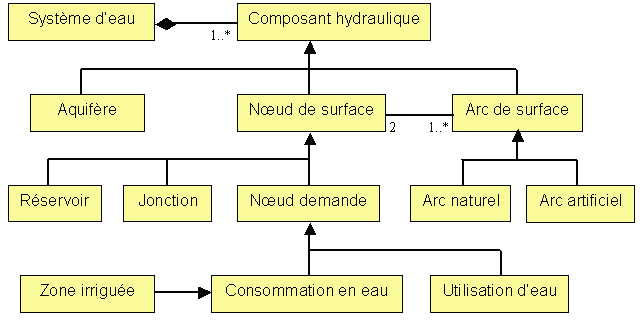
Description
Les systèmes considérés sont constitués d'éléments de stockage tant superficiels que souterrains, d'éléments de captage, de transport tant naturels qu'artificiels, d'utilisation et de consommation d'eau.
Les modèles proposés permettent la simulation continue du fonctionnement des systèmes basé sur des règles de gestion très souples. Ces consignes font référence à des priorités de distribution de demandes et une hiérarchisation de la mobilisation des ressources. La mobilisation s'effectue en respectant les courbes de remplissage objectif des réservoirs.
L'utilisation du modèle consiste à modifier, au fur et à mesure des simulations, les consignes de gestion pour améliorer la satisfaction des objectifs.
Formulation
Nous reprenons, ici et au niveau de chacun des composants, la formulation mathématique définie dans le programme WARSYP [WARSYP 1998]. Cette formulation est axée vers l'optimisation de la gestion stratégique, mais elle permet de rendre explicite les caractéristiques des objets et les contraintes de gestion tactique.
Le problème consiste à minimiser une fonction objectif composée de termes pénalisation et de couts sur un horizon décisionnel, sachant les conditions formulées dans les équations (1)-(30) relatives aux divers composants ; les termes de pénalisation sont relatifs aux déficits ou aux déviations par rapport à des niveaux objectifs ; et les termes de couts sont relatifs aux pompages de surface ou dans les aquifères. La fonction objectif peut être exprimée comme suit :
{tex}\small \sum _{t \in T}\left[\sum _{i \in NE}\sum _{m \in M+it}\lambda^+_{imt.} V^+_{imt}+\sum _{i \in NE}\sum _{m \in M-it}\lambda^-_{imt.} V^-_{imt} + \\ \sum _{(e,f) \in NAN} \alpha_{eft.}Q^-_{eft}+ \sum _{n \in ND \cup NC}\sum _{f \in Fn} \delta_{nft.}D^-__{nft.}+ \sum _{n \in NS Ynt.}S^-_{nt} \\ +\sum _{k \in NR} \sigma_{kt}.R^-_{kt}+ \sum _{k \in NP} \sum _{n \in Nk} \mu_ {knt.} Y_{knt}+\sum _{(e,f) \in NA} \phi_{eft.}Q_{eft}+\ \\ \sum _{i \in NC} \omega_i (\sum _{f \in Pi}Q_{ift}- (d_{it}- \sum _{l \in Fi}D^-_{ilt})) \right]{/tex}
Le stockage dans le réservoir et les aquifères et la limitation des déficits cumulés des demandes nécessitent un couplage multipériodes, qui conduit à l'adoption d'un modèle complexe de résolution d'équations linéaires.
Définition
Propriétés structurales
| # Systeme | en-tête avec le nom du type d'objet |
| nom | label de l'objet |
| description | texte de complément d'information |
Propriétés de gestion
| simulation | index de simulation (1..99). Les fichiers de simulation stockent les propriétés de gestion et les résultats relatifs à un même système d'eau. |
| mode | processus de simulation - 1 à 3 simulation de la gestion tactique en mois, décades, jours respectivement - |
| periodes | année début ; mois début (1..12) ; nombre de mois de l'horizon décisionnel pour l'optimisation, 1 sinon ; nombre de mois de simulation |
| ecoulement | répertoire des données d'apports - unité : hm3 |
| lame ecoulee | répertoire des données d'apports exprimées en lames - unité : m |
| sorties | type des résultats à sauvegarder. Les chroniques annuelles et les cumuls mensuels sont toujours stockés. La sauvegarde des autres chroniques - mois, décades, jours - est optionnelle. |
Exemple
# Systeme
nom Amenagements_A2
description amenagements "1995" - Bras de Sable - AEP 50%
simulation 2
mode 2.decade
periodes 1962 1 1 348
ecoulement C:\ActiveHyd\guadelou\flows\hm3\
lame ecoulee C:\ActiveHyd\guadelou\flows\m\
sorties global an mois decade jour

Figure B2.1. - Système d'eau - graphique associé
Ensembles principaux
| {tex}\small NT{/tex} | pas de temps successifs de l'horizon décisionnel |
| {tex}\small NE{/tex} | ensemble des réservoirs, soit des noeuds de surface avec une capacité de stockage |
| {tex}\small ND{/tex} | ensemble des noeuds demandes |
| {tex}\small NC{/tex} | ensemble des noeuds demandes non consommatrices. {tex}\small NC = NCF \cup NCE{/tex}, où |
| {tex}\small NCF{/tex} | ensemble des noeuds demandes non consommatrices sans capacité de stockage associé |
| {tex}\small NCE{/tex} | ensemble des noeuds demandes non consommatrices associés à des réservoirs, {tex}\small NCE \subset NE{/tex} |
| {tex}\small NS{/tex} | ensemble des noeuds demandes qui requièrent un volume de stockage réservé dans des réservoirs amont, {tex}\small NS \subseteq ND\cup NC{/tex} |
| {tex}\small NJ{/tex} | ensemble des noeuds jonctions |
| {tex}\small NU{/tex} | ensemble des noeuds pompages |
| {tex}\small NN{/tex} | ensemble des noeuds de surface, {tex}\small NN=NE\cup ND\cup NCF\cup NJ\cup NU{/tex} |
| {tex}\small NK{/tex} | ensemble des aquifères, noeuds souterrains avec une capacité de stockage |
| {tex}\small NA{/tex} | ensemble des arcs de surface |
| {tex}\small NAN{/tex} | ensemble des arcs naturels, {tex}\small NAN\subset NA {/tex} |
| {tex}\small NAB{/tex} | ensemble des arcs artificiels, {tex}\small NAB\subset NA {/tex} |
| {tex}\small \Gamma {/tex} | ensemble des pas de temps successifs utilisés pour controler le déficit cumulé de demande en eau sur ces périodes pour chaque demande et chaque période |
Ensembles secondaires
| {tex}\small M_i {/tex} | ensemble des zones correspondant au découpage du réservoir i pour chaque période |
| {tex}\small F_n {/tex} | ensemble des niveaux correspondant au découpage de la demande en eau du noeud n, {tex}\small n\in ND \cup NC {/tex} |
| {tex}\small P_e \subset NN {/tex} | ensemble des noeuds directement à l'aval du noeud e, {tex}\small e \in NN-ND {/tex}. Si {tex}\small f \in P_e {/tex}, {tex}\small (e,f) \in NA{/tex} |
| {tex}\small P_e^{\prime} \subset NN {/tex} | ensemble des noeuds à l'aval du noeud e, {tex}\small e \in NN-ND{/tex} |
| {tex}\small Q_f \subset NN-ND {/tex} | ensemble des noeuds directement à l'amont du noeud f, {tex}\small f \in NN{/tex}. Si {tex}\small Q_f {/tex}, {tex}\small (e,f) \in NA{/tex} |
| {tex}\small Q_f^{\prime}\subset NN-ND{/tex} | ensemble des noeuds à l'amont du noeud f, {tex}\small f \in NN{/tex} |
| {tex}\small NR{/tex} | ensemble des aquifères avec recharge artificielle |
| {tex}\small N^k \subseteq NJ{/tex} | ensemble des noeuds jonctions qui permettent la recharge artificielle de l'aquifère k, {tex}\small k \in NR{/tex} |
| {tex}\small N^k \subseteq Np{/tex} | ensemble des aquifères avec pompage des demandes en eau |
| {tex}\small N_k \subseteq ND {/tex} | ensemble des noeuds demandes avec pompage possible dans l'aquifère k, {tex}\small k \in NP{/tex} |
| {tex}\small J_k \subset NE \cup NJ{/tex} | ensemble des réservoirs ou des noeuds jonctions avec échange avec l'aquifère k, {tex}\small k \in NK{/tex} |
| {tex}\small k(i){/tex} | aquifère en relation avec le réservoir ou la jonction i, {tex}\small i \in NE \cup NJ{/tex} |
| {tex}\small j(n){/tex} | noeud jonction vers lequel l'eau du noeud demande n est partiellement restituée au système, {tex}\small n \in ND{/tex} |
Paramètres d'état
| {tex}\small b_{it}{/tex} | apport extérieur au réservoir ou au noeud jonction i au pas de temps t, {tex}\small i \in NE \cup NJ{/tex}, {tex}\small t \in NT{/tex}. Si le noeud i est en tête du bassin, c'est à dire s'il n'a pas de noeud en amont, bit représente l'apport naturel. Mais s'il y a des noeuds plus en amont, bit représente l'écoulement net, correspondant à l'apport naturel du bassin intermédiaire à l'aval des noeuds amont. |
| {tex}\small r_{kt}{/tex} | recharge extérieure de l'aquifère k pour le pas de temps t, {tex}\small k \in NK{/tex}, {tex}\small t \in NT{/tex} |
| {tex}\small V_{i0}{/tex} | valeur du stockage du réservoir i au début de l'horizon décisionnel, {tex}\small i \in NE{/tex} |
| {tex}\small Z_{k0}{/tex} | valeur du stockage de l'aquifère k au début de l'horizon décisionnel, {tex}\small k \in NK{/tex} |
| {tex}\small V^{m+}it V^{m-}it{/tex} |
capacités de stockage maximale et minimale du réservoir i au pas de temps t, {tex}\small i \in NE{/tex}, {tex}\small t \in NT{/tex} |
| {tex}\small V^{m+}imt {/tex} | capacité maximale de stockage de la zone m du réservoir i au pas de temps t, {tex}\small m \in M_i{/tex}, {tex}\small i \in NE{/tex}, {tex}\small t \in NT{/tex}tel que {tex}\small V^{m+}it = V^{m+}iMt{/tex} |
| {tex}\small Z^{m+}k Z^{m-}k{/tex} | capacité de stockage maximale et minimale de l'aquifère k, {tex}\small k \in NK{/tex} |
| {tex}\small f^eit{/tex} | coefficient de perte par évaporation par rapport au volume stocké dans le réservoir i pour le pas de temps t, iÎNE, tÎNT |
| {tex}\small f^1it{/tex} | coefficient de perte par infiltration profonde par rapport au volume stocké dans le réservoir i pour le pas de temps t, {tex}\small i \in NE{/tex}, {tex}\small t \in NT{/tex} |
| {tex}\small f^1jt{/tex} | coefficient de perte en ligne non récupérable par rapport au volume transité dans la jonction j pour le pas de temps t, {tex}\small j \in NJ{/tex}, {tex}\small t \in NT{/tex} |
| {tex}\small f^iit{/tex} | coefficient de perte par infiltration dans l'aquifère k(i) par rapport au volume stocké dans le réservoir i pour le pas de temps t, {tex}\small i \in NE{/tex}, {tex}\small t \in NT{/tex} |
| {tex}\small f^ijt{/tex} | coefficient de perte par infiltration dans l'aquifère k(j) par rapport au volume transité dans la jonction j pour le pas de temps t, {tex}\small j \in NJ{/tex}, {tex}\small t \in NT{/tex} |
| {tex}\small f^fkit{/tex} | coefficient de réalimentation du réservoir ou du noeud jonction j par rapport au volume stocké dans l'aquifère k pour le pas de temps t, {tex}\small k \in NK{/tex}, {tex}\small i \in J_k{/tex}, {tex}\small t \in NT{/tex} |
| {tex}\small q^{m+}eft{/tex} | limite supérieure de transit dans l'arc de surface (e, f), pour {tex}\small (e,f) \in NA-NAB{/tex} |
| {tex}\small \rho _n{/tex} |
coefficient de restitution de la demande en eau du noeud demande n vers la jonction {tex}\small j(n){/tex}, {tex}\small n \in ND{/tex} |
| {tex}\small \xi^\tau n{/tex} | fraction de demande en eau cumulée sur t pas de temps, dont le déficit est très fortement pénalisé, {tex}\small n \in ND \cup NC{/tex}, {tex} \small \tau \in \Gamma{/tex} |
| {tex}\small P^{m+}ut{/tex} | limite supérieure de pompage du noeud u pour le pas de temps t, {tex}\small u \in NU{/tex}, {tex}\small t \in NT{/tex} |
| {tex}\small P^{m+}uet{/tex} | limite supérieure de transit dans l'arc artificiel (u, e) pour le pas de temps t, {tex} \small (u,e) \in NAB {\tex}, {tex}\small u \in NU{/tex}, {tex}\small t \in NT{/tex} |
| {tex}\small R^{m+}kt{/tex} | limite supérieure de recharge artificielle de l'aquifère k pour le pas de temps t, {tex}\small k \in NU{/tex}, {tex}\small t \in NT{/tex} |
| {tex}\small X^{m+}jkt{/tex} | limite supérieure de recharge artificielle de l'aquifère k à partir du noeud jonction j pour le pas de temps t, {tex}\small k \in NU{/tex}, {tex}\small j \in N^k{/tex} , {tex}\small t \in NT{/tex} |
| {tex}\small m^{m+}kt{/tex} | limite supérieure de pompage dans l'aquifère k pour le pas de temps t, {tex}\small k \in NP{/tex}, {tex}\small t \in NT{/tex} |
| {tex}\small y^{m+}knt{/tex} | limite supérieure de pompage de la demande n dans l'aquifère k pour le pas de temps t, {tex}\small k \in NU{/tex}, {tex}\small N \in n_K{/tex}, {tex}\small t \in NT{/tex} |
Paramètres de niveaux objectifs
| {tex}\small \eta _{it}{/tex} |
niveau de stockage objectif du réservoir i pour le pas de temps t, {tex}\small i \in NE{/tex}, {tex}\small t \in NT{/tex} |
| {tex}\small M^+ _{it}{/tex} | = { {tex}\small m \in M_i / V^{m+}_{it} > \eta_{it}{/tex}, pour {tex}\small i \in NE{/tex}, {tex}\small t \in NT{/tex}} |
| {tex}\small M^- _{it}{/tex} | = {{tex}\small m \in M_i / V^{m+}_{it} \leq \eta_{it}{/tex}, pour {tex}\small i \in NE{/tex}, {tex}\small t \in NT{/tex}} |
| {tex}\small d_{nt}{/tex} | demande en eau du noeud demande n et pour le pas de temps t, {tex}\small n \in ND \cup NC{/tex}, {tex}\small t \in NT{/tex} |
| {tex}\small s_{nt}{/tex} | volume de stockage réservé objectif dans les réservoirs amont pour satisfaire de futur besoins potentiels au noeud demande n pour le pas de temps t, {tex}\small n \in NS{/tex}, {tex}\small t \in NT{/tex} |
| {tex}\small q^{m-}_{eft}{/tex} | débit réservé associé à l'arc naturel (e, f) pour le pas de temps t, {tex}\small (e,f) \in NAN{/tex} {tex}\small t \in NT{/tex} |
| {tex}\small r^{m-}_{kt}{/tex} | volume de recharge artificielle objectif de l'aquifère k pour le pas de temps t, {tex}\small k \in NR{/tex}, {tex}\small t \in NT{/tex} |
Paramètres de pénalisation
| {tex}\small \lambda^+imt, \lambda^-imt{/tex} |
coefficient de pénalités sur l'écart positif et négatif par rapport au stockage objectif du niveau de stockage dans la zone m du réservoir i pour le pas de temps t, {tex}\small t \in NT{/tex}, {tex}\small t \in NT{/tex}, et {tex}\small m \in M^+it{/tex}et {tex}\small m \in M^-it{/tex}respectivement |
| {tex}\small \delta_{nft}{/tex} |
coefficient de pénalités sur le déficit de la demande de niveau f dans le noeud demande n pour le pas de temps t, {tex}\small n \in ND \cup NC{/tex}, {tex}\small f \in F_n{/tex}, {tex}\small t \in NT{/tex}. |
| Si le niveau 1 correspond au niveau le plus proche de la demande objectif, on a {tex}\small \delta_{nlt} \leq \delta_{n2t} ...\delta_{nFnt}{/tex} |
|
| {tex}\small \gamma_{nt}{/tex} | coefficient de pénalités sur le déficit de stockage réservé dans les réservoirs amont pour satisfaire de futur besoins potentiels au noeud demande n pour le pas de temps t, {tex}\small n \in NS{/tex}, {tex}\small t \in NT{/tex} |
| {tex}\small \alpha_{eft}{/tex} |
coefficient de pénalités sur le déficit de débit réservé relatif à l'arc naturel (e, f) pour le pas de temps t, {tex}\small (e,f) \in NA{/tex}, {tex}\small t \in NT{/tex} |
| {tex}\small \sigma_{kt}{/tex} | coefficient de pénalités sur le déficit de recharge artificielle de l'aquifère k pour le pas de temps t, {tex}\small k \in NR{/tex}, {tex}\small t \in NT{/tex} |
| {tex}\small \phi_{eft}{/tex} | coefficient de cout de transit dans l'arc de surface (e, f) pour le pas de temps t, {tex}\small (e,f) \in NA{/tex}, {tex}\small t \in NT{/tex} |
| {tex}\small \mu_{knt}{/tex} | coefficient de cout de pompage de la demande n dans l'aquifère k pour le pas de temps t, {tex}\small k \in NP{/tex}, {tex}\small n \in NK{/tex}, {tex}\small t \in NT{/tex} |
| {tex}\small \omega_{it}{/tex} |
coefficient de pénalités de déversement au niveau d'une demande non consommatrice i pour le pas de temps t, {tex}\small i \in NC{/tex}, {tex}\small t \in NT{/tex} |
| {tex}\small V_{it}{/tex} | volume stocké dans le réservoir i pour le pas de temps t, {tex}\small i\in NE {/tex}, {tex}\small t\in NT {/tex} |
| {tex}\small V^+_{imt}{/tex} | volume de stockage en excès par rapport au stockage objectif dans la zone m du réservoir i pour le pas de temps t, {tex}\small m\in M^+_{it}{/tex}, {tex}\small i\in NE {/tex}, {tex}\small t\in NT {/tex} |
| {tex}\small V^-_{imt}{/tex} | mÎvolume de stockage en déficit par rapport au stockage objectif dans la zone m du réservoir i pour le pas de temps t, {tex}\small m\in M^-_{it}{/tex}, {tex}\small i\in NE {/tex}, {tex}\small t\in NT {/tex} |
| {tex}\small S_{int}{/tex} | volume de stockage réservé dans le réservoir i pour satisfaire des besoins futurs potentiels de la demande n pour le pas de temps t, {tex}\small n\in NS {/tex}, {tex}\small i\in NE {/tex}, {tex}\small t\in NT {/tex} |
| {tex}\small Z_{kt}{/tex} | volume stocké dans le réservoir k pour le pas de temps t, {tex}\small k\in NK {/tex}, {tex}\small t\in NT {/tex} |
| {tex}\small Q_{eft}{/tex} | flux d'eau dans l'arc de surface (e, f) pour le pas de temps t, {tex}\small (e,f)\in NA{/tex}, {tex}\small t\in NT {/tex} |
| {tex}\small X_{jkt} {/tex} | volume de recharge artificielle de l'aquifère k à partir du noeud jonction j pour le pas de temps t, {tex}\small k\in NR {/tex}, {tex}\small j\in N^k{/tex}, {tex}\small t\in NT {/tex} |
| {tex}\small Y_{knt} {/tex} | volume pompé de la demande n dans l'aquifère k pour le pas de temps t, {tex}\small k\in NP {/tex}, {tex}\small n\in N_k{/tex}, {tex}\small t\in NT {/tex} |
| {tex}\small D^-\{nft} {/tex} | déficit de demande en eau dans le niveau f du noeud demande n pour le pas de temps t, {tex}\small n\in ND \cup NC{/tex}, {tex}\small f\in F_n{/tex} , {tex}\small t\in NT {/tex} |
| {tex}\small S^-_{nt}{/tex} | déficit sur le stockage réservé pour satisfaire de futurs besoins potentiels de la demande n pour le pas de temps t, {tex}\small n\in NS{/tex}, {tex}\small t\in NT {/tex} |
| {tex}\small Q^-_{eft}{/tex} | déficit sur le débit réservé associé à l'arc naturel (e, f) pour le pas de temps t, {tex}\small (e,f)\in NAN{/tex}, {tex}\small t\in NT {/tex} |
| {tex}\small R^-_{kt}{/tex} | déficit sur la recharge artificielle de l'aquifère k pour le pas de temps t, {tex}\small n\in NS{/tex}, {tex}\small t\in NT {/tex} |
Réservoir
Description
Un réservoir est considéré comme un noeud de surface possédant une capacité de stockage.
A chaque pas de temps, le volume d'eau stocké dans un réservoir est diminué des pertes par évaporation et infiltration et augmenté par les dessertes des arcs amont, par les apports nets naturels, et éventuellement par réalimentation souterraine. Le volume net est en partie déversé en aval et en partie stocké pour le pas de temps suivant.
Le réservoir peut être découpé en zones où l'on pénalisera plus ou moins des déficits et des surplus de stockage par rapport à une courbe objectif. Il est par exemple ainsi possible de définir une tranche de stockage d'eau de moindre qualité qu'il faut au maximum éviter de solliciter ou de constituer un creux pour l'amortissement des crues.
Formulation
Bilan en eau dans les réservoirs {tex}\small \forall i \in NE{/tex}, {tex}\small t \in NT{/tex}
| {tex}\small V ^prime_{it} = V_{it-1}+ \sum _{e \in Q_i}Q_{eit}+ b_{it}{/tex} | (1a) | |
| {tex}\small V^\prime{it}- f^e_{it.}V_{it}-f^1_{it}V_{it}+f^\prime_{it.}-i^\prime_{it.} = \sum _{j \in Pi} Q_{ijt} + V_{it}{/tex} | (1b) | |
| où | {tex}\small f^ \prime _{it} = f^f_{kit.}Z_{kt-1}{/tex} si {tex}\small\exists k / i \in J_k {/tex} 0, sinon |
(1c) |
| et |
{tex}\small i^ \prime = f^i_{it.}V_{it}.V_{it}{/tex} si {tex}\small k(i) \not=0{/tex}
0, sinon |
(1d) |
| et | {tex}\small V^{m-}it \leq V_{it} \leq V ^{m+}it{/tex} | (2) |
Déficits et surplus de stockage par rapport à une courbe objectif
| {tex}\small V_it = \eta _ {it}+ \sum _{m \in M+it} V^+ _{imt} - \sum _{m \in M-it} V^- _{imt} {/tex} |
(3) | ||
| où | {tex}\small V^+ _{imt}\leq V^{m++}_{imt} = V^{m+}_{im} - \eta it {/tex} {tex}\small V^{m+}_{imt} - V^{m+}_{im-1t}{/tex} , si {tex}\small \eta _{it} < V^{m+}_{im-1t}{/tex} |
{tex}\small \forall m \in M^+_{it}{/tex} | (4) |
| et | {tex}\small V^-_{imt} \leq V^{m+-}_{imt} = \eta _{it}-V^{m+}_{imt}{/tex} {tex}\small V^{m+}_{im+1t}-V^{m+}_{imt}{/tex} , si {tex}\small V^{m+}_{im+1t}\leq \eta _{it}{/tex} |
{tex}\small \forall m \in M^-_{it}{/tex} | (5) |
Note : Les différents termes sont décrits dans les ensembles d'objets , les paramètres et les variables du modèle.
Définition
Propriétés structurales
| # Reservoir | en-tête avec le nom du type d'objet |
| nom | label de l'objet |
| index | identificateur entier du noeud de surface |
| localisation | coordonnées (x, y) du noeud de surface |
| Courbe de remplissage | |
| hauteurs | nombre de points n (2..12) de la courbe de remplissage |
| hauteur | n valeurs de niveau - unité : m |
| surface | n valeurs de surface du plan d'eau - unité : ha |
| stockage | n valeurs de stockage - unité : hm3 |
| apport naturel | nom de la chronique d'apport, coefficient correcteur |
| L evaporation | variation mensuelle interannuelle de la lame d'eau évaporée (L=V/S.Cev) - unité : m |
| pluie directe | nom de la chronique d'apport sous forme de lame, coefficient correcteur |
Propriétés de gestion
| C perte | variation mensuelle interannuelle des coefficients de pertes par infiltration profonde - voir équations (1a)-(1b) |
| infiltration | 0 si pas d'infiltration, index a de l'aquifère sinon et dans ce cas nous avons la définition suivante |
| C infiltration | variation mensuelle interannuelle des coefficients de pertes par infiltration dans l'aquifère a |
| stockage objectif | variation mensuelle interannuelle du stockage objectif - unité : hm3 |
| Découpage en zones | |
| zones | nombre de zones considérées M (1..5). Pour chaque zone m, nous avons les 3 définitions suivantes |
| volume m | variation mensuelle interannuelle de la limite supérieure de stockage de la zone m (1..M) - unité : hm3 |
| penalites positives m | variation mensuelle interannuelle des pénalités associées au surplus de stockage par rapport à l'objectif de la zone m (1..M) |
| penalites negatives m | variation mensuelle interannuelle des pénalités associées au déficit de stockage par rapport à l'objectif de la zone m (1..M) |
| stockage initial | niveau de stockage initial - unité : hm3 |
| sorties | type des résultats à sauvegarder. Les chroniques annuelles et les cumuls mensuels sont toujours stockés. La sauvegarde des autres chroniques - mois, décades, jours - est optionnelle. |
Exemple
# Reservoir
nom Letaye
index noeud 1
localisation 55.30 43.40
hauteurs 9
hauteur 18 19 20 21 22 23 24 25 26
surface 0 1.44 3.53 5.99 8.7 11.63 14.74 18.01 21.43
stockage 0 0.006 0.031 0.078 0.151 0.253 0.385 0.548 0.745
apport naturel LETAYE 1
L evaporation 0.123 0.131 0.162 0.167 0.169 0.17 0.175 0.166 0.142 0.126 0.107 0.109
pluie directe RETENUE1 1
C perte 0.04 0.04 0.04 0.04 0.04 0.04 0.04 0.04 0.04 0.04 0.04 0.04
infiltration 0
stockage objectif 0.55 0.55 0.55 0.55 0.55 0.55 0.55 0.55 0.55 0.55 0.55 0.55
zones 2
volume 0 0 0 0 0 0 0 0 0 0 0 0 0
volume 1 0.05 0.05 0.05 0.05 0.05 0.05 0.05 0.05 0.05 0.05 0.05 0.05
volume 2 0.745 0.745 0.745 0.745 0.745 0.745 0.745 0.745 0.745 0.745 0.745 0.745
penalites positives 1 0 0 0 0 0 0 0 0 0 0 0 0
penalites negatives 1 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000
penalites positives 2 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000
penalites negatives 2 2.95 2.95 2.95 2.95 2.95 2.95 2.95 2.95 2.95 2.95 2.95 2.95
stockage initial 0.5
sorties global an mois

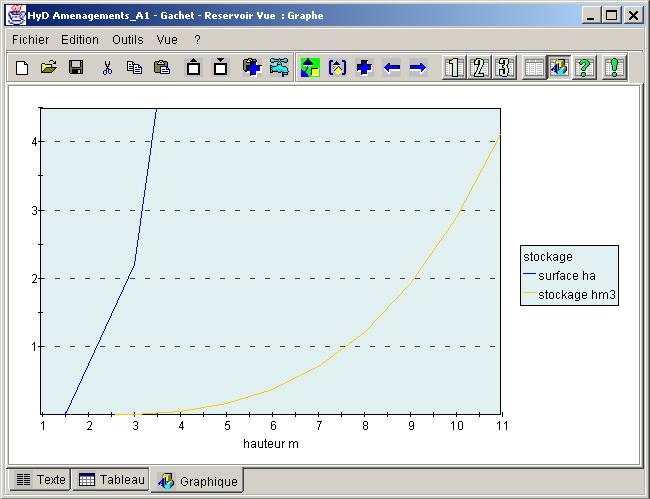
Figure B6.1. - Réservoir - graphique associé
Description
Une jonction est un noeud de surface où l'écoulement connaît une modification : confluence, prise en rivière, apport intermédiaire, etc.
Pour chaque pas de temps, le volume d'eau entrant à un noeud jonction correspond à la desserte par les arcs amont et éventuellement aux apports nets naturels, à la réalimentation par un aquifère et à la restitution d'une partie d'une demande. Le volume sortant correspond à l'alimentation des arcs aval et éventuellement aux pertes par infiltration et à la recharge artificielle d'un aquifère.
Formulation
Bilan en eau dans les jonctions {tex} \small\forall j{\in}NJ, t{\in}NT {/tex}
| {tex}\small F_{jt} = \rho_{jt}^{\prime} + \sum_{e\in Q_j}Q_{ejt} + f_{jt}^{\prime} + b_{jt} {/tex} | (6a) | |
| où | {tex}\small p^\prime jt = p_n \sum _{f \in Fn (d_{nft}+ D^-{nft}){/tex} si {tex}\small \exists i \in ND / j=j(n){/tex} 0, sinon |
(6b) |
| et | {tex}\small f^\prime jt = f^f_{kjt}.Z_{kt-1} {/tex} si {tex}\small \exists k / i \in J_k{/tex} 0, sinon |
(6c) |
| et | {tex}\small F_{jt}-f^ljt.F_{jt} = \sum _{f \in P_jQ_{jft}+ \chi_{jt}+ i^\prime_{jt}{/tex} |
(6d) |
| où | {tex}\small \chi_{jt} = X_{jkt}{/tex} si {tex}\small \exists k \in NR / j \in N^k{/tex} 0, sinon |
(6e) |
| {tex}\small i^\prime = f^i_{jt}.F_{jt}{/tex} si {tex}\small k(j) \not= 0{/tex} 0, sinon |
(6f) |
Note : Les différents termes sont décrits dans les ensembles d'objets , les paramètres et les variables du modèle.
Définition
Propriétés structurales
| # Jonction | en-tête avec le nom du type d'objet |
| nom | label de l'objet |
| index | identificateur entier du noeud de surface |
| localisation | coordonnées (x, y) du noeud de surface |
| apport naturel | nom de la chronique d'apport, coefficient correcteur |
Propriétés de gestion
| C perte | variation mensuelle interannuelle des coefficients de pertes par infiltration profonde - voir équations (6a)-(6d) |
| infiltration | 0 si pas d'infiltration, index a de l'aquifère sinon et dans ce cas nous avons la définition suivante |
| C infiltration | variation mensuelle interannuelle des coefficients de pertes par infiltration dans l'aquifère a - voir équations (6a)-(6f) - |
| sorties | type des résultats à sauvegarder. Les chroniques annuelles et les cumuls mensuels sont toujours stockés. La sauvegarde des autres chroniques - mois, décades, jours - est optionnelle. |
Exemple
# Jonction
nom vernou
index noeud 3
localisation 17.60 27.21
apport naturel TRAVERSE 0.64
C perte 0 0 0 0 0 0 0 0 0 0 0 0
infiltration 0
sorties global an mois

Figure B7.1. - Jonction - graphique associé
Pompage
Description
Un pompage est un noeud de surface où une certaine quantité d'eau peut être dérivée vers des arcs artificiels.
Pour chaque pas de temps, le volume d'eau entrant correspond à la desserte par les arcs amont. Le volume sortant correspond à l'alimentation des arcs aval, avec une limite supérieure pour la desserte des arcs artificiels.
Formulation
Bilan en eau dans les pompages et les demandes non consommatrices {tex}\small \forall i \in NCF \cup NU {/tex}, {tex}\small t \in NT {/tex}
| {tex}\small \sum _{(u,e) \in NAB}Q_{uet} \leq p^{m+}ut{/tex} | (7) |
Contrainte de limite de pompage {tex}\small \forall u \in NU{/tex}, {tex}\small t\in NT {/tex}
| {tex}\small \sum _{(u,e) \in NAB}Q_{uet} \leq p^{m+}ut{/tex} |
(23) | ||
| où | {tex}\small 0 \leq Q_{uet} \leq p^{m+}_{uet}{/tex} |
{tex}\small \forall (u,e) \in NAB{/tex} | (24) |
Note : Les différents termes sont décrits dans les ensembles d'objets , les paramètres et les variables du modèle.
Définition
Propriétés structurales
| # Pompage | en-tête avec le nom du type d'objet |
| nom | label de l'objet |
| index | identificateur entier du noeud de surface |
| localisation | coordonnées (x, y) du noeud de surface |
Propriétés de gestion
| limite | variation mensuelle interannuelle de la limite supérieure de pompage - unité : hm3 |
| sorties | type des résultats à sauvegarder. Les chroniques annuelles et les cumuls mensuels sont toujours stockés. La sauvegarde des autres chroniques - mois, décades, jours - est optionnelle. |
Exemple
# Pompage
nom Pompa1
index noeud 1
localisation 5.00 5.00
limite 3 3 3 3 3 3 3 3 3 3 3 3
sorties global an mois

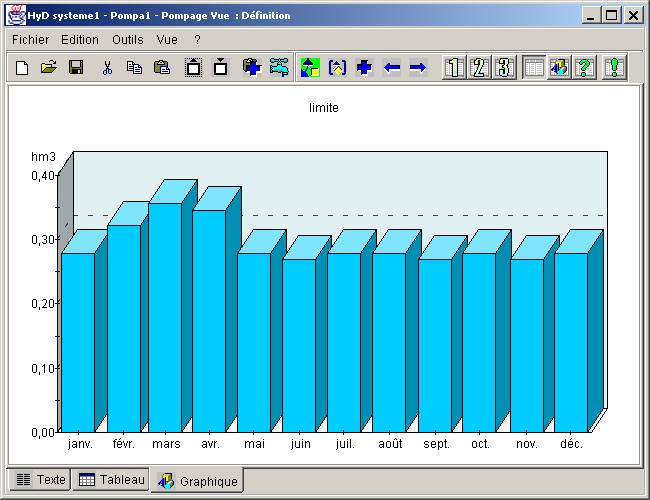
Figure B8.1. - Pompage - graphique associé
Description
Une consommation en eau est un noeud de surface correspondant à une demande où l'eau est consommée totalement ou partiellement : demande urbaine, demande industrielle, demande d'irrigation, etc.
Pour chaque pas de temps, le volume d'eau entrant correspond à la desserte par les arcs amont et éventuellement au pompage dans un aquifère. Le volume sortant correspond à la restitution éventuelle d'une partie de l'eau au système à partir d'un noeud jonction à l'aval de la demande.
La demande peut être découpée en différents niveaux où les déficits de desserte en eau sont pénalisés de manière croissante.
Formulation
Déficit de demande en eau{tex}\small \forall n \in ND{/tex}, {tex}\small t \in NT{/tex}
| {tex}\small y_{nt}+\sum_{e \in Q_n}Q_{ent} = d_{nt}-\sum_{f \in F_n}D^-_{nft}{/tex} | (15a) | ||
| où | {tex}\small y_{nt}=Y_{knt}{/tex} si {tex}\small \exists k \in NP / n \in N_k{/tex} 0, sinon |
(15b) | |
| et | {tex}\small 0 \leq D^-_{nft} \leq d^\prime _{nft}{/tex} | {tex}\small \forall f \in F_n{/tex}, {tex}\small n \in ND{/tex}, {tex}\small t \in NT{/tex} | (16) |
| où | {tex}\small d^\prime _{nft}{/tex} correspond à la demande en eau du niveau f, donc au déficit maximal pour ce niveau, tel que |
| {tex}\small \sum _{f\in F_n}d^\prime_{nft}= d_{nt}{/tex} | (17) |
Les contraintes suivantes ne sont utilisées que pour les modèles d'optimisation prenant en compte un horizon prévisionnel.
Limite de déficits cumulés dans des mois consécutifs {tex}\small \forall n \in ND, t=1,...,|NT|- \tau + 1, \tau \in \Gamma{/tex}
| {tex}\small \sum_1 \leq 0 \leq \tau \sum_{{f \in F_n}D^-_{nft + 0-1}}{/tex} | (26) | |
| et | {tex}\small 0 \leq \sum_{{f \in F_n}D^-_{nft} \leq d_{nt}{/tex} | (27) |
Volume réservé dans des réservoirs {tex}\small \forall i \in NE{/tex},{tex}\small t \in NT{/tex}
| {tex}\small \sum _{n \in P^\prime i \cap NS} S_{int} \leq V_{it} - V^{m-}it{/tex} |
(28) |
Déficit de stockage réservé dans des réservoirs amont pour satisfaire des besoins futurs potentiels {tex}\small \forall i \in NE{/tex}, {tex}\small t \in NT{/tex}
| {tex}\small \sum _{i \in Q^\prime n \cap NE} S_{int} = s_{nt}-S^-_{nt}{/tex} | (29) | |
| où | {tex}\small 0 \leq S^-_{nt} \leq s_{nt}{/tex} |
(30) |
Note : Les différents termes sont décrits dans les ensembles d'objets , les paramètres et les variables du modèle.
Définition
Propriétés structurales
| # Consommation en eau | en-tête avec le nom du type d'objet |
| nom | label de l'objet |
| index | identificateur entier du noeud de surface |
| localisation | coordonnées (x, y) du noeud de surface |
| Demande en eau | |
| demande | variation mensuelle interannuelle de la demande en eau - unité : hm3 |
| source | adresse et coefficient de la demande en eau de référence. Cette demande peut être une chronique de débits (ecoulement.nom de la chronique) ou une caractéristique (débit transité dans un lien, demande en eau, etc) d'un autre composant (type.nom du composant). Si elle existe, cette demande se substitue à la variation mensuelle interannuelle. |
| retour | 1 entier ; 1 réel : index du noeud de retour ; coefficient de restitution, valeur comprise entre 0 et 1 |
| aquifere | 0 si pas de pompage, index de l'aquifère sinon et dans ce cas nous avons les 2 définitions suivantes |
| limite de pompage | variation mensuelle interannuelle de la limite supérieure de pompage - unité : hm3 |
| cout de pompage | variation mensuelle interannuelle du cout fictif de pompage |
Propriétés de gestion
| Découpage en zones | |
| niveaux | nombre de niveaux de demandes F (1..5) . Pour chaque niveau f, nous avons les 2 définitions suivantes |
| taux f | variation mensuelle interannuelle de participation du niveau f (1..F) à la demande en eau - valeurs comprises entre 0 et 1 - pour chaque mois Somme(rate 1 .. rate F)=1 |
| penalites f | variation mensuelle interannuelle des pénalités associées aux déficits de niveau f (1..F) |
| restriction | conditionnement de la desserte à un indicateur, les demandes en eau correspondants aux niveaux associés à des pénalités inférieures ou égales à la pénalité limite ne seront pas desservies si la valeur de l'indicateur est inférieure à la valeur limite définie. L'indicateur peut être lu dans le fichier d'apports ou correspondre au stockage d'un réservoir, au volume transité dans un arc, etc. |
| sorties | type des résultats à sauvegarder. Les chroniques annuelles et les cumuls mensuels sont toujours stockés. La sauvegarde des autres chroniques - mois, décades, jours - est optionnelle. |
Exemple
# Consommation en eau
nom deshaut
index noeud 26
localisation 43.80 37.00
demande 0.62 0.7 0.775 0.75 0.62 0.6 0.62 0.62 0.6 0.62 0.6 0.62
source - 1
retour 0 0
aquifere 0
niveaux 2
taux 1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1
taux 2 0.9 0.9 0.9 0.9 0.9 0.9 0.9 0.9 0.9 0.9 0.9 0.9
penalites 1 4 4 4 4 4 4 4 4 4 4 4 4
penalites 2 5 5 5 5 5 5 5 5 5 5 5 5
restriction 0 0 -
sorties global an mois

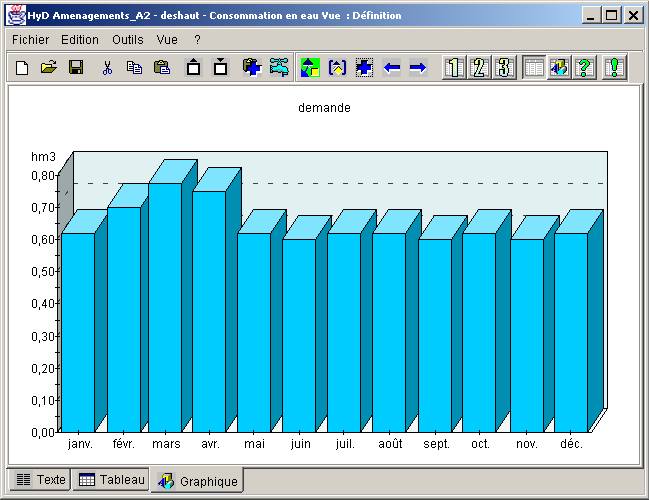
Figure B9.1. - Consommation en eau - graphique associé
Description
Une zone irriguée est une aire de consommation d’eau où le besoin est calculé à partir d’un bilan hydrique prenant en compte la réserve en eau du sol pour une culture.
Pour chaque pas de temps, le volume d'eau entrant correspond à la desserte par les arcs amont et éventuellement au pompage dans un aquifère. Le volume sortant correspond à la restitution éventuelle d'une partie de l'eau au système à partir d'un noeud jonction à l'aval de la demande.
La demande peut être découpée en différents niveaux où les déficits de desserte en eau sont pénalisés de manière croissante.
Bilan hydrique
Le modèle classique simple à réservoir a été retenu pour le calcul du bilan hydrique. On considère ainsi que toute la pluie arrivant sur le sol s'infiltre jusqu'à saturation du sol, qui correspond au remplissage du réservoir dont la capacité constitue la réserve utile (RU). Tout apport d'eau supérieur est considéré comme perdu : la partie correspondant à l'eau gravitaire le sera par percolation, le reste par ruissellement de surface.
Le bilan peut donc s'écrire simplement :
Niveau_reserve_final = Niveau_reserve_initial + Pluie + Dose_apport - ETR
où ETR : évapotranspiration réelle.
L'évapotranspiration
L'évapotranspiration réelle donne la consommation réelle de la culture en fonction du stress hydrique. Elle est difficile à évaluer, on se contente des résultats semi-empiriques visant à donner sa variation en fonction de l'humidité du sol ou plutôt en fonction de l'état de la réserve.
La réserve utile (RU) est décomposée en réserve facilement utilisable (RFU) et en réserve difficilement utilisable (RDU). RU et RFU dépendent de la profondeur du sol. Trois types de fonctions sont disponibles pour exprimer leurs variations dans l'année.
Tant qu'il y a de l'eau dans la RFU, c'est à dire que la réserve reste supérieure à la RDU, on considère que la plante reste à son niveau de consommation optimal, ETR = ETM. Lorsque la réserve R devient inférieure à RDU, on considère la relation ETR / ETM = R / RDU.
L'ETM, évapotranspiration maximale d'une culture, correspond donc à la consommation du périmètre planté quand celui-ci est convenablement approvisionné en eau.
Dans la pratique, ETM est calculé par ETM = Kc . ETP, où Kc, coefficient cultural, dépend du stade de développement du végétal.
On peut ainsi définir la variation du coefficient cultural au cours de l'année. L'ETP -EvapoTranspiration Potentielle - est définie à partir d'une (ou plusieurs) chroniques d'évaporation.
Demande en eau
Pour assurer une récolte optimale, il faut maintenir la réserve en eau à un niveau supérieur à la RDU. Mais la réserve ne doit pas être forcément pleine.
On a donc introduit la notion de niveau d'irrigation. Ce seuil est exprimé par le pourcentage de remplissage de RFU. Par convention il n'y a pas d'irrigation si la réserve en eau du sol est supérieure à ce seuil d'alerte ou si ce seuil est nul. Ce seuil peut être variable sur l'année.
Le volume de demande en eau peut ainsi s'exprimer :
Vol_demande = Deficit x Surface_irriguee / Efficience_apport
où Deficit : déficit hydrique par rapport à la réserve pleine
soit Deficit = max (Niveau_RFU - Niveau_reserve_initial + ETM - Pluie, 0)
où ETM : évapotranspiration maximale ;
Efficience_apport : rapport entre volume réellement utilisé et volume d'apport
Formulation
Déficit de demande en eau {tex}\small \forall n \in ND{/tex} , {tex}\small t \in NT{/tex}
| {tex}\small y_{nt} + \sum_{{e \in Q_n}Q_{ent}}=d_{nt}- \sum_{{f \in F_n}D^-_{nft}}{/tex} | (15a) | ||
| où | {tex}\small y_{nt}=Y_{knt}{/tex}si {tex}\small \exists k \in NP / n \in N^k{/tex} 0, sinon |
(15b) | |
| et | {tex}\small 0 \leq D^-_{nft} \leq d^\prime _{nft}{/tex} | {tex}\small \forall f \in F_n{/tex}, {tex}\small n \in ND {/tex}, {tex}\small t \in NT{/tex} | (16) |
| où | {tex}\small d^\prime _{nft}{/tex}correspond à la demande en eau du niveau f, donc au déficit maximal pour ce niveau, tel que | ||
| {tex}\small \sum _{{f \in F_n}d^\prime_{nft}}= d_{nt}{/tex} | (17) |
Note : Les différents termes sont décrits dans les ensembles d'objets , les paramètres et les variables du modèle.
Définition
Propriétés structurales
| # Zone irriguee | en-tête avec le nom du type d'objet |
| nom | label de l'objet |
| index | identificateur entier du noeud de surface |
| localisation | coordonnées (x, y) du noeud de surface |
| Demande en eau | |
| surface | surface irriguée - unité : ha |
| pluie | adresses et coefficients de participation des stations pluviométriques (max 6) |
| evaporation | variation mensuelle interannuelle de l'ETP EvapoTranspiration Potentielle - unité : m |
| Kc | coefficient cultural |
| ru | réserve utilisable - unité : m |
| rfu | réserve facilement utilisable - unité : m |
| prof.rac. | profondeur racinaire - unité : m |
| niveau | niveau d'irrigation, valeur comprise entre 0 et 1 - si 0 alors pas d'irrigation - 1 correspond au maintien de la RFU pleine |
| efficience | taux d'apport : efficience * demande = deficit * surface |
| retour | 1 entier ; 1 réel : index du noeud de retour ; coefficient de restitution, valeur comprise entre 0 et 1 |
| aquifere | 0 si pas de pompage, index de l'aquifère sinon et dans ce cas nous avons les 2 définitions suivantes |
| limite de pompage | variation mensuelle interannuelle de la limite supérieure de pompage - unité : hm3 |
| cout de pompage | variation mensuelle interannuelle du cout fictif de pompage |
Propriétés de gestion
| Découpage en zones | |
| niveaux | nombre de niveaux de demandes F (1..5) . Pour chaque niveau f, nous avons les 2 définitions suivantes |
| taux f | variation mensuelle interannuelle de participation du niveau f (1..F) à la demande en eau - valeurs comprises entre 0 et 1 - pour chaque mois Somme(rate 1 .. rate F)=1 |
| penalites f | variation mensuelle interannuelle des pénalités associées aux déficits de niveau f (1..F) |
| restriction | conditionnement de la desserte à un indicateur, les demandes en eau correspondants aux niveaux associés à des pénalités inférieures ou égales à la pénalité limite ne seront pas desservies si la valeur de l'indicateur est inférieure à la valeur limite définie. L'indicateur peut être lu dans le fichier d'apports ou correspondre au stockage d'un réservoir, au volume transité dans un arc, etc. |
| sorties | type des résultats à sauvegarder. Les chroniques annuelles et les cumuls mensuels sont toujours stockés. La sauvegarde des autres chroniques - mois, décades, jours - est optionnelle. |
Exemple
# Zone irriguee
nom ban_Pcov
index noeud 147
localisation 27.36 21.01
surface 2000
pluie DUMANOIR 0.24 NEUFCHAT 0.23 DOUVIRFA 0.21 NESTY 0.12 MOREAU 0.12 BOISDEBO 0.08
evaporation 0.108 0.107 0.152 0.137 0.162 0.164 0.149 0.139 0.131 0.149 0.101 0.091
Kc 1.1 1.1 1.1 1.1 1.1 1.1 1.1 1.1 1.1 1.1 1.1 1.1
ru 0.036
rfu 0.012
prof.rac. 1 1 1 1 1 1 1 1 1 1 1 1
niveau 1 1 1 1 1 1 1 1 1 1 1 1
efficience 1
retour 0 0
aquifere 0
niveaux 2
taux 1 0.2 0.2 0.2 0.2 0.2 0.2 0.2 0.2 0.2 0.2 0.2 0.2
taux 2 0.8 0.8 0.8 0.8 0.8 0.8 0.8 0.8 0.8 0.8 0.8 0.8
penalites 1 7 7 7 7 7 7 7 7 7 7 7 7
penalites 2 10 10 10 10 10 10 10 10 10 10 10 10
restriction 0 0 -
sorties global an mois

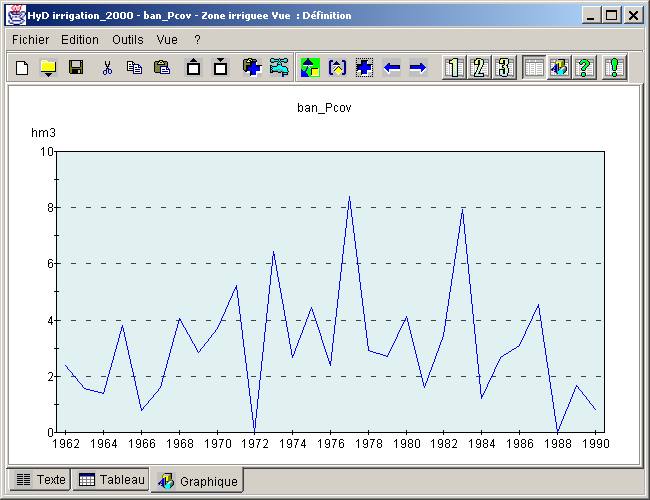
Figure B10.1. - Zone irriguée - graphique associé
Description
Une utilisation d'eau correspond à une demande non consommatrice. Elle associe une demande à un noeud de surface dont l'apport en eau est restitué complètement au système : centrale hydro-électrique, définition de droits d'eau, etc. La demande peut être découpée en différents niveaux où les déficits de desserte en eau sont pénalisés de manière croissante.
Formulation
Bilan en eau dans les pompages et les demandes non consommatrices {tex}\forall i \in NC \cup NU{/tex}, {tex}\small t \in NT{/tex}
| {tex}\small \sum _{{e \in Q_i}Q_{eit} = \sum _{{f \in Pi}Q_{ift}}{/tex} | (7) |
Déficit dans les demandes non consommatrices {tex} \small \forall i \in NC {/tex}, {tex}\small t \in NT{/tex}
|
{tex}\small \sum _{{f \in Pi}Q_{ift}} \geq d_{it} - \sum _{{l \in Fi}D^-_{ilt}}{/tex}
|
(12) | ||
| et | {tex}\small 0 \leq D^-{ilt} \leq d^\prime_{ilt}{/tex} | {tex}\small \forall l \in F_i{/tex} | (13) |
| où | {tex}\small d^\prime_{ilt}{/tex} est la limite supérieure de déficit pour le niveau l | tel que | |
| {tex}\small \sum _{{l \in Fi}d^\prime_{ilt}=d_{it}}{/tex} | (14) |
Note : Les différents termes sont décrits dans les ensembles d'objets , les paramètres et les variables du modèle.
Définition
Propriétés structurales
| # Utilisation d'eau | en-tête avec le nom du type d'objet |
| nom | label de l'objet |
| index | identificateur entier du noeud de surface |
| localisation | coordonnées (x, y) du noeud de surface |
| Demande en eau | |
| demande | variation mensuelle interannuelle de la demande en eau - unité : hm3 |
| source | adresse et coefficient de la demande en eau de référence. Cette demande peut être une chronique de débits (ecoulement.nom de la chronique) ou une caractéristique (débit transité dans un lien, demande en eau, etc) d'un autre composant (type.nom du composant). Si elle existe, cette demande se substitue à la variation mensuelle interannuelle. |
Propriétés de gestion
Découpage en zones
| niveaux | nombre de niveaux F de découpage de la demande en eau. Pour chaque niveau f, nous avons les 2 définitions suivantes |
| taux f | variation mensuelle interannuelle de participation du niveau f (1..F) à la demande en eau - valeurs comprises entre 0 et 1 - pour chaque mois Somme(rate 1 .. rate F)=1 |
| penalites f | variation mensuelle interannuelle des pénalités associées aux déficits de niveau f (1..F) |
| restriction | conditionnement de la desserte à un indicateur, les demandes en eau correspondants aux niveaux associés à des pénalités inférieures ou égales à la pénalité limite ne seront pas desservies si la valeur de l'indicateur est inférieure à la valeur limite définie. L'indicateur peut être lu dans le fichier d'apports ou correspondre au stockage d'un réservoir, au volume transité dans un arc, etc. |
| sorties | type des résultats à sauvegarder. Les chroniques annuelles et les cumuls mensuels sont toujours stockés. La sauvegarde des autres chroniques - mois, décades, jours - est optionnelle. |
Exemple
# Utilisation d'eau
nom AepInTrav
index noeud 39
localisation 19.03 31.64
demande 2.2 2 2.2 2.1 2.2 2.1 2.2 2.2 2.1 2.2 2.1 2.2
source - 0
niveaux 1
taux 1 1 1 1 1 1 1 1 1 1 1 1 1
penalites 1 2 2 2 2 2 2 2 2 2 2 2 2
restriction 0 0 -
sorties global an mois

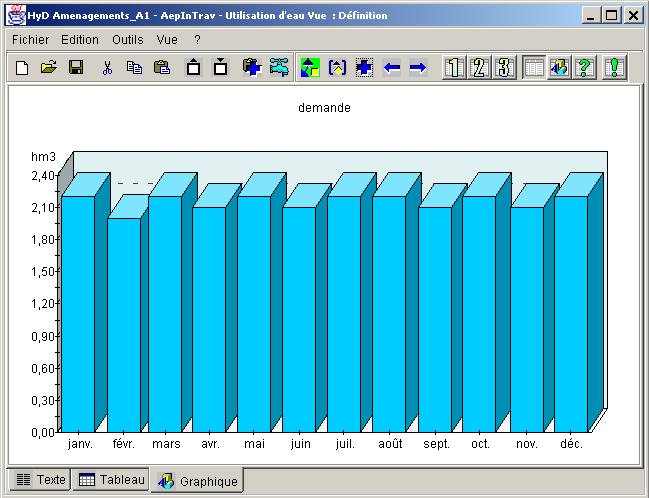
Figure B11.1. - Utilisation d'eau - graphique associé
Aquifère
Description
Un aquifère est considéré comme un noeud souterrain possédant une capacité de stockage.
Pour chaque pas de temps, le volume d'eau entrant à un aquifère correspond aux apports extérieurs naturels, à l'infiltration à partir de réservoirs ou de noeuds de jonction et éventuellement à de la recharge artificielle à partir d'un noeud jonction. Le volume sortant correspond à la réalimentation de réservoirs ou de noeuds de jonction et à des pompages si le volume net de l'aquifère les permet.
Formulation
Bilan en eau dans les aquifères {tex}\small \forall k \in NK{/tex}, {tex}\small t \in NT{/tex}
| {tex}\small Z_{kt-1}+ \sum _ {{j \in Nk}/k \in NR X_jkt} + \sum _{{j \in NJ / k(j) = k f^i_{jt}F_jt}} + \sum _ {{i \in NE} / k(i)} = k f^i_{it} V ^\prime_{it}+ r_{kt} = \sum _{{n \in N_k}/k \in NP Y_{knt} + f^\prime _{kt}+ Z_{kt}}{/tex} | (8a) | |
| où | {tex}\small f^\prime _{kt}= \sum _{i \in NE \cup NJ / i \in Jk f^fkitZ_{kt-1}{/tex} si {tex}\small J_k \not = \not \bigcirc{/tex} 0, sinon | (8b) |
| et | {tex}\small Z^{m-} \leq Z_{kt} \leq Z^{m+}k{/tex} | (9) |
Déficit de recharge artificielle {tex}\small \forall k \in NR{/tex}, {tex}\small t \in NT{/tex}
| {tex}\small r^{m-}kt - R^-kt \leq \sum j \in Nk Xjkt \leq r^{m+}kt{/tex} | (18) | |
| où | {tex}\small 0 \leq Xjkt \leq x^{m+}jkt{/tex} | (19) |
| et | {tex}\small 0 \leq R^-kt \leq r^{m-}kt{/tex} | (20) |
Limite de pompage dans les aquifères {tex}\small \forall k \in NP{/tex}, {tex}\small t \in NT{/tex}
| {tex}\small \sum _{n \in Nk Yknt \leq m^{m+}kt{/tex} | (21) | |
| où | {tex}\small Y_{knt} \leq y^{m+}knt{/tex} | (22) |
Note : Les différents termes sont décrits dans les ensembles d'objets , les paramètres et les variables du modèle.
Définition
Propriétés structurales
| # Aquifere | en-tête avec le nom du type d'objet |
| nom | label de l'objet |
| index | identificateur entier de l'aquifère |
| localisation | coordonnées (x, y) du noeud de surface |
| stockage mini | capacité minimale de stockage - unité : hm3 |
| stockage maxi | capacité maximale de stockage - unité : hm3 |
| apport naturel | nom de la chronique d'apport, coefficient correcteur |
Propriétés de gestion
| Transfert vers la surface | |
| noeuds sortie | nombre de noeuds de surface avec échange d'eau - Pour chaque noeud, nous avons les 2 définitions suivantes |
| noeud sortie | index i du noeud de surface |
| C sortie | variation mensuelle interannuelle des coefficients d'échange relatifs au réservoir ou à la jonction i - voir équations (8a)-(8b) |
| pompage | variation mensuelle interannuelle des limites supérieures de pompage - unité : hm3 |
| Recharge artificielle | |
| recharge totale | variation mensuelle interannuelle des limites supérieures de recharge artificielle - unité : hm3 |
| noeuds recharge | nombre de noeuds de recharge - Pour chaque noeud, nous avons les 2 définitions suivantes |
| noeud recharge | index j du noeud de recharge |
| limite recharge | variation mensuelle interannuelle des limites supérieures de recharge depuis le noeud jonction j - unité : hm3 |
| recharge objectif | variation mensuelle interannuelle des volumes objectifs de recharge artificielle - unité : hm3 |
| penalites recharge | variation mensuelle interannuelle des pénalités associées aux déficits de recharge artificielle |
| stockage initial | niveau de stockage initial - unité : hm3 |
| sorties | type des résultats à sauvegarder. Les chroniques annuelles et les cumuls mensuels sont toujours stockés. La sauvegarde des autres chroniques - mois, décades, jours - est optionnelle. |
Exemple
# Aquifere
nom Aquif1
index noeud 1
localisation 5.00 5.00
stockage mini 0
stockage maxi 0
apport naturel - 1
noeuds sortie 1
noeud sortie 1
C sortie 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1
pompage 0 0 0 0 0 0 0 0 0 0 0 0
recharge totale 0 0 0 0 0 0 0 0 0 0 0 0
noeuds recharge 1
noeud recharge 1
limite recharge 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1
recharge objectif 0 0 0 0 0 0 0 0 0 0 0 0
penalites recharge 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1
stockage initial 0
sorties global an mois

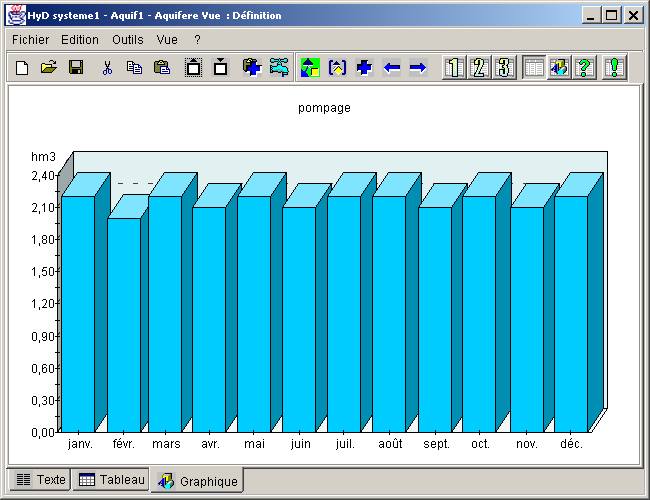
Figure B12.1. - Aquifère - graphique associé
Arc de surface
Description
Un arc de surface est un lien qui assure le transit d'eau entre 2 noeuds de surface : un noeud amont et un noeud aval.
Formulation
Limite de transit dans les arcs {tex}\small \forall (e,f) \in NA-NAN{/tex}, {tex}\small t \in NT{/tex}
| {tex}\small 0 \leq Q_{eft} \leq q^{m+}_{eft}{/tex} | (25) |
Note : Les différents termes sont décrits dans les ensembles d'objets , les paramètres et les variables du modèle.
Définition
Propriétés structurales
| # Arc | en-tête avec le nom du type d'objet |
| nom | label de l'objet |
| noeuds | index des noeuds de surface amont et aval |
Propriétés de gestion
| flux max | variation mensuelle interannuelle des limites supérieures de flux d'eau - unité : hm3 |
| sorties | type des résultats à sauvegarder. Les chroniques annuelles et les cumuls mensuels sont toujours stockés. La sauvegarde des autres chroniques - mois, décades, jours - est optionnelle. |
Exemple
# Arc
nom c900_lez
noeuds 8 28
flux max 4.018 3.629 4.018 3.888 4.018 3.888 4.018 4.018 3.888 4.018 3.888 4.018
sorties global an mois

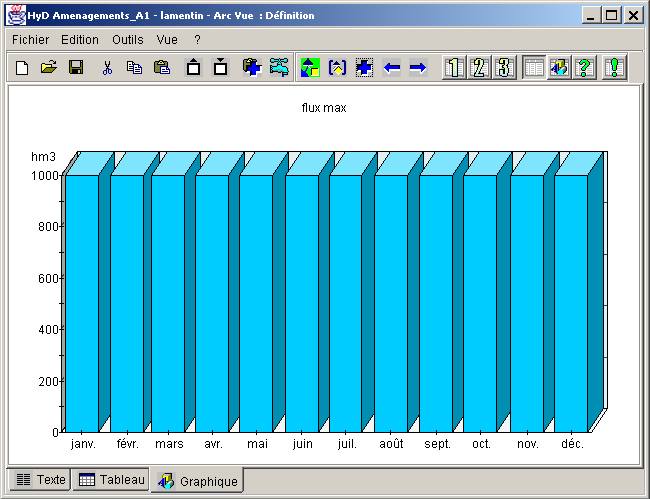
Figure B13.1. - Arc de surface - graphique associé
Arc naturel
Description
Un arc naturel est un lien qui assure l'écoulement entre 2 noeuds du bassin hydrographique. On lui associe généralement un débit réservé qui peut varier au cours de l'année.
Formulation
Déficit sur le débit réservé {tex}\small \forall (e,f) \in NAN{/tex}, {tex}\small t \in NT{/tex}
| {tex}\small q^{m-}_{eft}-Q^-_{eft} \leq Q_{eft}{/tex} | (10) | |
| et | {tex}\small 0 \leq Q^-_{eft} \leq q^{m-}_{eft}{/tex} | (11) |
Note : Les différents termes sont décrits dans les ensembles d'objets , les paramètres et les variables du modèle.
Définition
Propriétés structurales
| # Arc naturel | en-tête avec le nom du type d'objet |
| nom | label de l'objet |
| noeuds | index des noeuds de surface amont et aval |
Propriétés de gestion
| flux max | variation mensuelle interannuelle des limites supérieures de flux d'eau - unité : hm3 |
| flux min | variation mensuelle interannuelle des débits réservés - unité : hm3 |
| penalites | variation mensuelle interannuelle des pénalités associées aux déficits sur les débits réservés |
| sorties | type des résultats à sauvegarder. Les chroniques annuelles et les cumuls mensuels sont toujours stockés. La sauvegarde des autres chroniques - mois, décades, jours - est optionnelle. |
Exemple
# Arc naturel
nom vernou
noeuds 6 7
flux max 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000 1000
flux min 0.375 0.339 0.375 0.363 0.375 0.363 0.375 0.375 0.363 0.375 0.363 0.375
penalites 1 1 1 1 1 1 1 1 1 1 1 1
sorties global an mois

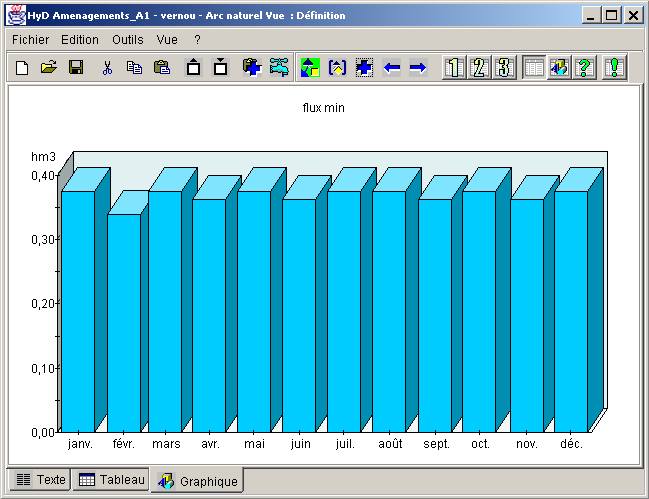
Figure B14.1. - Arc naturel - graphique associé
Arc artificiel
Description
Un arc artificiel est un lien qui assure le transit d'eau, entre 2 noeuds de surface, sous une certaine limite : canal, conduite, etc.
Les arcs artificiels peuvent être associés à un pompage qui introduit une autre limite de prélèvement.
Formulation
Limite de transit dans les arcs {tex}\small \forall (e,f) \in NA-NAN{/tex}, {tex}\small t \in NT{/tex}
| {tex}\small 0 \leq Q_{eft} \leq q^{m+}_{eft}{/tex} |
(25) |
Note : Les différents termes sont décrits dans les ensembles d'objets , les paramètres et les variables du modèle.
Définition
Propriétés structurales
| # Arc artificiel | en-tête avec le nom du type d'objet |
| nom | label de l'objet |
| noeuds | index des noeuds de surface amont et aval |
Propriétés de gestion
| flux max | variation mensuelle interannuelle des limites supérieures de flux d'eau - unité : hm3 |
| sorties | type des résultats à sauvegarder. Les chroniques annuelles et les cumuls mensuels sont toujours stockés. La sauvegarde des autres chroniques - mois, décades, jours - est optionnelle. |
Exemple
# Arc artificiel
nom Arc a1
noeuds 1 2
flux max 2.491 2.25 2.491 2.411 2.491 2.411 2.491 2.491 2.411 2.491 2.411 2.491
sorties global an mois








